可逆数字水印时期通过利用多媒体信息中存在的冗余， 将水印信息(如载体特征信息、版权信息等)镶嵌到数字多媒体载体当中， 并可在经受方完好地索要水印且无损地恢收复始载体[1].该时期可用于媒体的内容标志、完好性认证和版权保护等功能男同 動漫， 已等闲应用于对躲闪性、安全性以及保真度要求较高的限制， 如军事及医学图像、法律秘书图片等[2].基于图像的可逆水印算法主要不错分为以下四大类:无损压缩[3]、差值膨大[4]、直方图平移[5]以及展望谬误膨大[6].可逆数字水印时期一般不接洽水印的鲁棒性， 现存的大浩荡可逆水印算法在受到噪声搅扰或经过处理后无法正确地索要镶嵌的水印.试验中， 含水印的数字多媒体在麇集等信谈中传输时， 不可幸免地会遭到各式处理或搅扰， 是以， 在好多应用场景中但愿镶嵌的水印具有一定的鲁棒性， 在含水印的载体未受到信号处理或坏心报复时， 在经受方简略正确地索要水印和无损地恢收复始载体; 而在含水印的载体经过一些信号处理操作时， 在经受端仍然简略正确地索要水印.近几年来， 鲁棒可逆水印时期冉冉成为了信息荫藏限制的一个伏击的接头标的， 已取得一些有道理的适度[7-13].

跟着互联网时期和云打算时期的快速发展， 用户可通过互联网将贵府和数据上传到汉典处事器或云表进行存储， 当需要时再下载使用.云存储纯粹了购买储存设备的开支并升迁了获取资源的便利性.另外， 云处事中心的浩荡打算才气使得用户不错享受到第三方提供的数据处理等处事.但是， 云打算时期在便捷东谈主们生计的同期， 也激发了数据安全和秘籍保护的问题[14].数据加密当作保护多媒体内容秘籍的一种格式， 不错在上传到云表之前先对数据进行加密， 有用地裁汰内容秘籍表现的风险.为了对云表中海量的加密数据进行有用经管和安全保护， 云表经管者但愿将一些用户贵府关系的信息镶嵌到密文数据中， 并通过索要镶嵌的信息来完竣密文检索和数据保护.因此， 加密域可逆水印时期成为了连年来大数据云打算布景下信息荫藏限制的接头热门.加密域可逆水印时期衔尾加密时期和可逆水印时期的优点， 在不融会明文内容的情况下径直将水印镶嵌到密文载体中， 并在解密及信息索要后能无损地恢收复始载体.当今的加密域图像可逆水印算法主要分为两大类:基于对称加密系统的可逆水印算法[15， 16]和基于非对称加密系统的可逆水印算法[17-20].当今， 加密域中的可逆水印算法绝大浩荡都不具有鲁棒性， 而在一些云打算的应用场景中， 信息荫藏者但愿镶嵌的水印信息不仅具有可逆性， 而且具有一定的鲁棒性， 以便在解密后图像受到处理或报复时仍能认证媒体的版权.

与对称加密系统比较， 同态加密系统为非对称加密系统， 安全性更高， 且允许对密文进行算术运算， 更适应用于云打算布景下的第三方数据处理.本文衔尾同态加密系统和鲁棒可逆水印时期， 提倡了一种基于同态加密系统的图像鲁棒可逆水印算法.该算法最初对原始图像进行8×8分块， 并利用Paillier加密系统[21]进行加密得到密文图像.在加密域中， 通过模乘法逆元MMI(modular multiple inverse)要道和查询密文映射表来得到每个密文分块的统计量， 然后利用同态特色对统计量进行直方图平移镶嵌水印.在经受方可分别在含水印的密文图像或解密图像中得到统计量直方图并索要水印， 同期， 通过对统计量进行与镶嵌进程相背的直方图平移往返应密文图像或原始图像.另外， 解密后含水印的图像在受到一定进度的图像处理操作(如JPEG/JPEG 2000压缩和叠加高斯噪声等)后仍能正确地索要水印.该算法完竣了在分歧原始图像进行预处理的情况下可径直在加密后的密文图像中镶嵌水印， 并可分别从加密域或明文域索要水印和回应密文图像或原始图像， 而且镶嵌的水印对常见的图像处理操作具有一定的鲁棒性.本文算法镶嵌失真较小， 鲁棒性邃密， 具有填塞的镶嵌容量来镶嵌加密图像关系标签信息、版权信息或图像特征信息等， 适用于云打算中加密图像的内容标志、完好性认证及版权保护.

1 Paillier加密系统

Paillier加密系统[21]是一种加性同态公钥加密系统， 这种加密时期已等闲应用于加密信号处理或第三方数据处理限制.其同态特色发扬为:在加密后可径直对密文进行相应的算术运算， 其运算适度与明文域中对应的运算适度一致.其概率特色发扬为:关于调换的明文， 可通过不同的加密进程得到不同的密文， 从而保证了密文的语义安全.其加密息争密机制如下.

密钥生成:立地遴荐两个较大的质数p和q， 打算它们的乘积N以及p-1、q-1的最小公倍数λ.然后再立地中式一个整数$ g \in Z_{{N^2}}^* $， 且g知足:

$ gcd\left( {L\left( {{g^\lambda }\bmod {N^2}} \right)， N} \right) = 1 $ (1)

其中， 函数L(u)=(u–1)/N， 函数gcd(·)用于打算两数的最大左券数， ZN2为小于N2的整数的衔尾， 而$ Z_{{N^2}}^* $为ZN3中与N2互质的整数的衔尾.(N， g)和λ分别为公钥和私钥.

加密进程:立地中式一个整数$ r \in Z_N^*， $关于大肆一个明文m∈ZN， 利用公钥(N， g)加密后得到对应密文c为

$ c = E[m， r] = {g^m} \cdot {r^N}\bmod {N^2} $ (2)

把柄Paillier加密系统的性质， 密文$ c \in Z_{{N^2}}^* $.利用调换的公钥进行加密时， 由于r的中式是立地的， 关于并吞个明文m， 可得到不同的密文c.但是解密后不错还原出调换的明文m， 从而保证了密文的语义安全.

解密进程:利用私钥λ， 对密文c解密后得到对应的明文m:

$ m = D\left[c \right] = \frac{{L\left( {{c^\lambda }\bmod {N^2}} \right)}}{{L\left( {{g^\lambda }\bmod {N^2}} \right)}}\bmod N $ (3)

另外， Paillier加密系统具有两个伏击的性质.

定理1.当g知足公式(1)时， 则c=E[m， r]是双射的， 即$ \forall \left( {m， r} \right)|m \in {Z_N}， r \in Z_N^* $都有独一的$ c = E\left[{m， r} \right] $与之逐一双应.也即是说， 关于两个明文$ {m_1}， {m_2} \in ZN $和$ \forall {r_1}， {r_2} \in Z_N^* $， 把柄公式(2)分别得到对应的密文$ {c_1}， {c_2} \in Z_{{N^2}}^* $， 则当且仅当m1=m2和r1=r2时， 等式c1=c2开荒.

本文将利用该定理完竣查询密文映射表得到密文分块统计量.

同态乘法性质:关于两个明文$ {m_1}， {m_2} \in ZN $和$ \forall {r_1}， {r_2} \in Z_N^* $， 对应密文$ {c_1} = E[{m_1}， {r_1}]， {c_2} = E[{m_2}， {r_2}] $知足:

$ {c_1} \cdot {c_2} = E[{m_1}， {r_1}] \cdot E[{m_2}， {r_2}] = {g^{{m_1} + {m_2}}} \cdot {\left( {{r_1} \cdot {r_2}} \right)^N}\bmod {N^2} $ (4)

解密后得到:

$ D{\rm{[}}{c_1} \cdot {c_2}{\rm{]}} = D\left[{E\left[{{m_1}， {r_1}} \right] \cdot E\left[{{m_2}， {r_2}} \right]\bmod {N^2}} \right] = {m_1} + {m_2}\bmod N $ (5)

本文将利用该性质对密文分块统计量进行直方图平移， 完竣在加密域中镶嵌水印信息.

2 同态加密域图像鲁棒可逆水印算法

本文提倡的基于同态加密系统的图像鲁棒可逆水印算法框架如下文图 1所示.最初， 数据通盘者对原始图像进行8x8分块， 并利用公钥(N， g)、密钥Ks和Paillier加密系统进行加密得到密文图像.信息荫藏者在加密域中利用Ks模乘法逆元MMI要道和查询相应密文映射表得到每个密文分块的统计量， 然后利用镶嵌密钥(T， G)对统计量进行直方图平移镶嵌水印.在经受方利用与镶嵌进程调换的要道， 可在加密域中得到含水印的加密图像的统计量直方图， 然后利用(T， G)索要水印并通过与镶嵌进程相背的直方图平移回应密文图像.在经受方利用私钥l可对含水印的加密图像进行解密并得到统计量直方图， 然后利用(T， G)可从未受到报复或图像处理的图像中索要水印和恢收复始图像， 或者从受到一定进度报复的图像中索要水印.

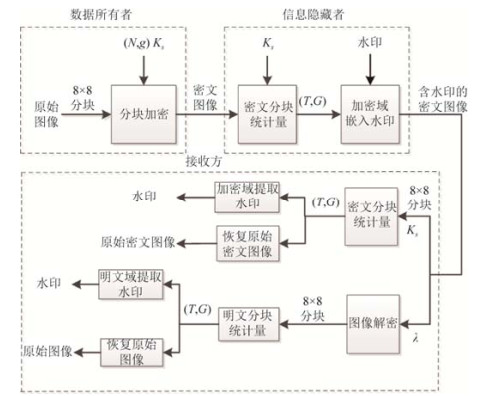Fig. 1 Sketch of the proposed robust and reversible image watermarking algorithm in encrypted image based on homomorphic cryptosystem 图 1 基于同态加密系统的图像鲁棒可逆水印算法框架 2.1 图像分块加密

数据通盘者最初把原始图像I分为些许个互不重迭的大小为8×8的明文分块， 记第k个明文分块为P(k).然后按照第1节Paillier加密系统中描述的加密进程， 立地中式一个整数$ {r_1}(k) \in Z_N^* $， 对P(k)中的每个明文像素值P(k)(i， j)利用公钥(N， g)和r1(k)进行加密得到密文C(k)(i， j):

$ {C^{(k)}}(i， j) = E[{P^{(k)}}(i， j)， {r_1}(k)] = {g^{{P^{(k)}}(i， j)}} \cdot {r_1}{(k)^N}\bmod {N^2} $ (6)

其中， $ i \in [1， 8]， j \in [1， 8] $， 记P(k)加密后的密文分块为C(k).为了提上下文提倡的密文分块统计量的安全性， 数据通盘者把柄密钥Ks立地中式另外8×8个整数$ {r_{(i， j)}}(k) \in Z_N^* $对0进行同态加密， 记加密进程为$ E[0， {r_{(i， j)}}(k)] $， 并对C(k)中的密文$ {C^{(k)}}(i， j) $进行同态乘法:

$ {C'^{(k)}}(i， j) = {C^{(k)}}(i， j) \cdot E[0， {r_{(i， j)}}(k)] = {g^{{P^{(k)}}(i， j)}} \cdot {({r_1}(k) \cdot {r_{(i， j)}}(k))^N}\bmod {N^2} $ (7)

记改革后的密文为$ {C'^{(k)}}(i， j) $， 密文分块为$ {C'^{(k)}} $， 记$ D[{C'^{(k)}}(i， j)] $为$ {C'^{(k)}}(i， j) $解密后的适度， 把柄式(4)和式(5)， $ D[{C'^{(k)}}(i， j)] $知足:

$ D[{C'^{(k)}}(i， j)] = {P^{(k)}}(i， j)\bmod N $ (8)

因此， $ {C'^{(k)}} $中的密文$ {C'^{(k)}}(i， j) $仍然是明文像素值$ {P^{(k)}}(i， j) $的一种加密适度， $ {C'^{(k)}}(i， j) $分别由不同的$ {r_1}(k) \cdot {r_{(i， j)}}(k) $加密而成.在莫得密钥Ks的情况下， 将不成得到下文提倡的密文分块统计量.记加密后的图像为E[I].

2.2 信息镶嵌 2.2.1 模乘法逆元

Zheng[22]提倡了模乘法逆元MMI要道.关于两个互质的整数y和z， 存在整数θ知足:

$ \theta \cdot y = 1\bmod z $ (9)

称θ为y的模乘法逆元， θ可把柄膨大欧几里德算法[23]求得.利用MMI要道不错完竣模运算中的除法.设另一个整数x， v是对x和y的乘积进行模z运算的适度:

$ v = x \cdot y\bmod z $ (10)

当y已知时， 利用MMI要道可从v中求出x:

$ v \cdot \theta = x \cdot y \cdot \theta = x\bmod z $ (11)

信息荫藏者经受到加密图像E[I]后， 最初把E[I]分为些许个互不重迭的大小为8×8的密文分块， 则第k个密文分块为$ {C'^{(k)}} $.然后利用密钥Ks和MMI要道将$ {C'^{(k)}} $中的密文$ {C'^{(k)}}(i， j) $回应为$ {C^{(k)}}(i， j) $.具体要道如下所述:由第1节可知密文$ c \in Z_{{N^2}}^* $， 即$ E[0， {r_{(i， j)}}(k)]， {C^{(k)}}(i， j) $都与N2互质， 则可把柄膨大欧几里德算法求得$ E[0， {r_{(i， j)}}(k)] $的模乘法逆元$ {\theta _{Er}}(k)， {\theta _{Er}}(k) $知足:

$ {\theta _{Er}}(k) \cdot E[0， {r_{(i， j)}}(k)] = 1\bmod {N^2} $ (12)

由于$ {C'^{(k)}}(i， j) $是$ {C^{(k)}}(i， j) $和$ E[0， {r_{(i， j)}}(k)] $的乘积， 可通过$ {C'^{(k)}}(i， j) $和$ {\theta _{Er}}(k) $求得$ {C^{(k)}}(i， j) $:

$ {C'^{(k)}}(i， j) \cdot {\theta _{Er}}(k) = {C^{(k)}}(i， j) \cdot E[0， {r_{(i， j)}}(k)] \cdot {\theta _{Er}}(k) = {C^{(k)}}(i， j)\bmod {N^2} $ (13)

其中， $ i \in [1， 8]， j \in [1， 8] $.密文回应为$ {C^{(k)}}(i， j) $后得到原密文分块C(k).

2.2.2 密文分块统计量

Zeng[11]提倡了一种图像分块的统计量， 最初把图像分为些许个互不重迭的大小为m×n的明文分块， 然后界说一个大小为m×n的矩阵M:

$ M(i， j) = \left\{ \begin{array}{l} 1， {\rm{ }}\bmod {\rm{ }}(i， 2) = \bmod {\rm{ }}(j， 2)\\ - 1， {\rm{ }}\bmod {\rm{ }}(i， 2) \ne \bmod {\rm{ }}(j， 2) \end{array} \right. $ (14)

其中， $ i \in [1， m]， j \in [1， n]， \bmod {\rm{ }}(x， 2) $是模2运算的函数.例如， 大小为2×2的矩阵M如图 2所示.

Fig. 2 Block M sized 2×2 图 2 2×2矩阵M涌现图

记d(k)为第k个明文分块P(k)的统计量， P(k)(i， j)为P(k)中点(i， j)位置上的明文值， 则d(k)为

$ {d^{(k)}} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {({P^{(k)}}(i， j) \times M(i， j))} } $ (15)

在加密域中， 信息荫藏者在不具有私钥λ的情况下不成将密文解密得到相应的明文， 无法径直进行明文值的运算得到统计量d(k).因此， 本文利用MMI要道和查询相应密文映射表得到密文分块统计量， 其值与对应的明文分块统计量调换.记密文分块统计量为d， d(k)是第k个密文分块C(k)的统计量.最初， 把柄膨大欧几里德算法求出密文分块C(k)中密文C(k)(i， j)的模乘法逆元$ {\theta _{{C^{(k)}}(i， j)}}， {\theta _{{C^{(k)}}(i， j)}} $知足:

$ {\theta _{{C^{(k)}}(i， j)}} \cdot {C^{(k)}}(i， j) = 1\bmod {N^2} $ (16)

之后界说大小为8×8的矩阵M1和M2， 第k个矩阵$ {M_1}^{(k)} $和$ {M_2}^{(k)} $知足:

$ {M_1}^{(k)}(i， j) = \left\{ \begin{array}{l} {C^{(k)}}(i， j)， {\rm{ if }}\bmod {\rm{ }}(i， 2) = \bmod {\rm{ }}(j， 2)\\ {\theta _{{C^{(k)}}(i， j)}}，情欲禁地高清在线观看 \;\;\;{\rm{ if }}\bmod {\rm{ }}(i， 2) \ne \bmod {\rm{ }}(j， 2) \end{array} \right. $ (17) $ {M_2}^{(k)}(i， j) = \left\{ \begin{array}{l} {\theta _{{C^{(k)}}(i， j)}}， \;\;{\rm{ if }}\bmod {\rm{ }}(i， 2) = \bmod {\rm{ }}(j， 2)\\ {C^{(k)}}(i， j)， {\rm{ if }}\bmod {\rm{ }}(i， 2) \ne \bmod {\rm{ }}(j， 2) \end{array} \right. $ (18)

其中， $ i \in [1， 8]， j \in [1， 8] $.利用$ {M_1}^{(k)} $和$ {M_2}^{(k)} $不错打算出C(k)的密文学式的统计量$ {c_{d1}}(k) $和$ {c_{d2}}(k) $:

$ \left\{ \begin{array}{l} {c_{d1}}\left( k \right) = \prod\limits_{i = 1}^m {\prod\limits_{j = 1}^n {{M_1}^{(k)}(i， j)\bmod {N^2}} } \\ {c_{d2}}\left( k \right) = \prod\limits_{i = 1}^m {\prod\limits_{j = 1}^n {{M_2}^{(k)}(i， j)\bmod {N^2}} } \end{array} \right. $ (19)

然后通过密文学式的统计量cd1(k)和cd2(k)便可在密文映射表中查询出对应的统计量d(k).底下是相应的公式推导和讲明.为了便捷意会， 以分块大小为2×2的密文分块加以例如讲明.分块大小为2×2的第k个密文分块C(k)如图 3所示.

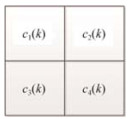Fig. 3 Cipher block C(k) sized 2×2 图 3 2×2密文分块C(k)涌现图

其中， $ i \in [1， 2]， j \in [1， 2] $， c1(k)， c2(k)， c3(k)， c4(k)分别是密文分块C(k)在点(i， j)位置上的密文C(k)(i， j).设c1(k)， c2(k)， c3(k)， c4(k)分别是由明文P1(k)， P2(k)， P3(k)， P4(k)加密而成， 而况对应的模乘法逆元为θ1(k)， θ2(k)， θ3(k)， θ4(k)， 它们知足:

$ \left\{ \begin{array}{l} {\theta _1}(k) \cdot {c_1}(k) = {\theta _1}(k) \cdot {g^{{P_1}(k)}} \cdot {r_1}{(k)^N} = 1\bmod {N^2}\\ {\theta _2}(k) \cdot {c_2}(k) = {\theta _2}(k) \cdot {g^{{P_2}(k)}} \cdot {r_1}{(k)^N} = 1\bmod {N^2}\\ {\theta _3}(k) \cdot {c_3}(k) = {\theta _3}(k) \cdot {g^{{P_3}(k)}} \cdot {r_1}{(k)^N} = 1\bmod {N^2}\\ {\theta _4}(k) \cdot {c_4}(k) = {\theta _4}(k) \cdot {g^{{P_4}(k)}} \cdot {r_1}{(k)^N} = 1\bmod {N^2} \end{array} \right. $ (20)

则密文分块C(k)的密文学式的统计量cd1(k)和cd2(k)为

$ \left\{ \begin{array}{l} {c_{d1}}(k) = \prod\limits_{i = 1}^2 {\prod\limits_{j = 1}^2 {{M_1}(i， j)} = {c_1}(k)} \cdot {\theta _2}(k) \cdot {\theta _3}(k) \cdot {c_4}(k) = {g^{{P_1}(k) + {P_4}(k)}} \cdot {r_1}{(k)^{2N}} \cdot {\theta _2}(k) \cdot {\theta _3}(k)\bmod {N^2}\\ {c_{d2}}(k) = \prod\limits_{i = 1}^2 {\prod\limits_{j = 1}^2 {{M_2}(i， j)} = {\theta _1}(k) \cdot {c_2}} (k) \cdot {c_3}(k) \cdot {\theta _4}(k) = {g^{{P_2}(k) + {P_3}(k)}} \cdot {r_1}{(k)^{2N}} \cdot {\theta _1}(k) \cdot {\theta _4}(k)\bmod {N^2} \end{array} \right. $ (21)

把柄Carmichael表面[21]， 关于$ \forall a \in Z_{{N^2}}^* $有:

$ {a^{N\lambda }} = 1\bmod {N^2} $ (22)

因此， 按照第1节Paillier加密系统的描述， 关于$ g \in Z_{{N^2}}^* $和$ {r_1}(k) \in Z_N^* $知足:

$ \left\{ \begin{array}{l} {g^{N\lambda }} = 1\bmod {N^2}\\ {r_1}{(k)^{N\lambda }} = 1\bmod {N^2} \end{array} \right. $ (23)

而况，

$ {g^{N\lambda }} \cdot {r_1}{(k)^{N\lambda }} = 1\bmod {N^2} $ (24)

把柄式(20)和式(24)， 不错推导出模乘法逆元的抒发式:

$ \left\{ \begin{array}{l} {\theta _1}(k) = {g^{N\lambda - {P_1}(k)}} \cdot {r_1}{(k)^{N(\lambda - 1)}}\bmod {N^2}\\ {\theta _2}(k) = {g^{N\lambda - {P_2}(k)}} \cdot {r_1}{(k)^{N(\lambda - 1)}}\bmod {N^2}\\ {\theta _3}(k) = {g^{N\lambda - {P_3}(k)}} \cdot {r_1}{(k)^{N(\lambda - 1)}}\bmod {N^2}\\ {\theta _4}(k) = {g^{N\lambda - {P_4}(k)}} \cdot {r_1}{(k)^{N(\lambda - 1)}}\bmod {N^2} \end{array} \right. $ (25)

把柄式(23)和式(25)中模乘法逆元的抒发式， 并接洽到统计量d(k)可能的取值， 公式(21)不错化简为

当$ {d^{(k)}} \ge 0 $时，

$ \left\{ \begin{array}{l} {c_{d1}}(k) = {g^{{P_1} - {P_2} + {P_4} - {P_3}}}\bmod {N^2}\\ {c_{d2}}(k) = {g^{2N\lambda + {P_2} - {P_1} + {P_3} - {P_4}}}\bmod {N^2} \end{array} \right. $ (26)

不然，

$ \left\{ \begin{array}{l} {c_{d1}}(k) = {g^{2N\lambda + {P_2} - {P_1} + {P_3} - {P_4}}}\bmod {N^2}\\ {c_{d2}}(k) = {g^{{P_1} - {P_2} + {P_4} - {P_3}}}\bmod {N^2} \end{array} \right. $ (27)

由于灰度图像中两个像素值差值的王人备值的取值鸿沟为0~255， 则关于每个2×2分块的统计量d(k)的王人备值的取值鸿沟为0~$255 \times \frac{{2 \times 2}}{2} $由于图像像素之间存在关系性， d(k)常常是一个较小的值(在本文实验中， 关于8×8分块d(k)的值均小于500).另外， 鄙人文中对统计量进行直方图平移镶嵌水印时， 会使d(k)产生大小为T+G的改革， 记统计量可能取值的王人备值为dp， 则$ {d_p} \in \left[{0， 255 \times \frac{{2 \times 2}}{2} + T + G} \right] $.利用公钥(N， g)， 当$ {d_p} \in {Z_N} $时不错加密得到:

$ {c_{{d_p}}} = {g^{{d_p}}}\bmod {N^2}， {d_p} = 0， 1， ...， 255 \times \frac{{2 \times 2}}{2} + T + G $ (28)

创建一个与dp逐一双应的密文映射表cdp如图 4所示.

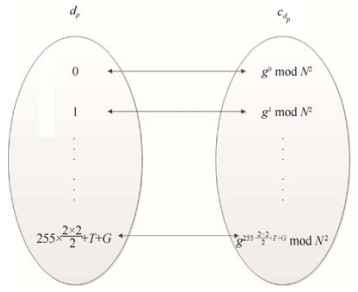Fig. 4 Mapping table cdp of dp 图 4 dp的密文映射表cdp

其中， 密文映射表cdp即是对通盘统计量可能取值的王人备值dp进行加密后得到的通盘密文值的衔尾.当$ {c_{d1}}(k) $与密文映射表cdp中的值$ {c_{{d_p}}}[x] $匹配时， 则标明$ {d^{(k)}} \ge 0 $， 得到$ {d^{(k)}} = {d_p}[x] $.当$ {c_{d2}}(k) $与密文映射表中的值cdp匹配时， 则标明$ {d^{(k)}} < 0 $， 得到$ {d^{(k)}} = - {d_p}[x] $.其中， $ x \in \left[{0， 255 \times \frac{{2 \times 2}}{2} + T + G} \right] $， 代表在密文映射表中的第x个值.因此， 信息荫藏者不错在莫得私钥l的情况下在加密图像中得到分块统计量d(k).

利用MMI要道和查询密文映射表的政策， 对大小为512×512的Lena灰度图像进行8×8分块和加密后得到的密文分块统计量d的直方图分散如图 5所示.

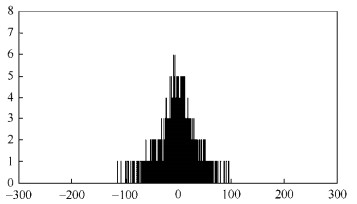Fig. 5 Histogram of statistical values of the encrypted Lena image blocks 图 5 Lena图像分块在加密后的统计量直方图 2.2.3 统计量直方图平移

信息荫藏者最初分别中式两个正整数T和G当作镶嵌密钥(T， G)， 其中， T＞dmax， dmax是统计量d中王人备值最大的数， 常常， T和G取为(8×8)/2的倍数.然后打算得到镶嵌所有B:

$ B = \left\lceil {\frac{{(T + G) \times 2}}{{8 \times 8}}} \right\rceil $ (29)

其中， 函数$ \left\lceil \cdot \right\rceil $为进取取整.通过对统计量d进行直方图平移， 不错把水印镶嵌到加密图像E[I]中， 每个8×8密文分块C(k)不错镶嵌1比特水印， 记镶嵌水印后的密文分块为矩阵$ C_w^{(k)} $.当镶嵌比特为0时， 不需要对C(k)进行处理， 即$ C_w^{(k)} = {C^{(k)}} $.当镶嵌比特为1时， 对C(k)中的密文$ {C^{(k)}}(i， j) $进行处理得到$ C_w^{(k)}(i， j) $:

$ C_w^{(k)}(i， j) = \left\{ \begin{array}{l} {C^{(k)}}(i， j) \cdot {g^B} =\\ {g^{{P^{(k)}}(i， j) + B}} \cdot {r_1}{(k)^N}\bmod {N^2}， {\rm{ if }}\;{d^{(k)}} \in [0， T){\rm{ and}}\bmod {\rm{ }}(i， 2) = \bmod {\rm{ }}(j， 2)\\ {C^{(k)}}(i， j) \cdot {g^B} =\\ {g^{{P^{(k)}}(i， j) + B}} \cdot {r_1}{(k)^N}\bmod {N^2}， {\rm{ if }}\;{d^{(k)}} \in (- T， 0){\rm{ and}}\bmod {\rm{ }}(i， 2) \ne \bmod {\rm{ }}(j， 2)\\ {C^{(k)}}(i， j)， \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ else}} \end{array} \right. $ (30)

其中， $ i \in [1， 8]， j \in [1， 8]， C_w^{(k)}(i， j) $为镶嵌水印后的密文.记$ P_w^{(k)}(i， j) $为$ C_w^{(k)}(i， j) $解密后的明文值， 加密域中的处理至极于在明文域中使明文像素值$ {P^{(k)}}(i， j) $变为$ {P_w}^{(k)}(i， j) $:

$ P_w^{(k)}(i， j) = \left\{ \begin{array}{l} {P^{(k)}}(i， j) + B， {\rm{if }}\;{\rm{ }}{d^{(k)}} \in [0， T){\rm{ and}}\bmod {\rm{ }}(i， 2) = \bmod {\rm{ }}(j， 2)\\ {P^{(k)}}(i， j) + B， {\rm{if }}\;{\rm{ }}{d^{(k)}} \in (- T， 0){\rm{ and}}\bmod {\rm{ }}(i， 2) \ne \bmod {\rm{ }}(j， 2)\\ {P^{(k)}}(i， j)， \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ else }} \end{array} \right. $ (31)

记镶嵌水印后的密文分块Cw(k)的统计量为dw(k)镶嵌比特0后， dw(k)在鸿沟(-T， T)内， 因此， 称(-T， T)为比特0区; 镶嵌比特1后， d(k)发生大小为平移量T+G的改革， 使dw(k)在鸿沟$ [- 2T- G， - T - G) $或$ [T + G， 2T + G) $内， 因此， 称$ [- 2T- G， - T - G) $和$ [T + G， 2T + G) $为比特1区.通常， 为了升迁统计量的安全性， 利用密钥Ks对含Cw(k)中的密文按照公式(7)与$ E[0， {r_{(i， j)}}(k)] $进行同态乘法得到矩阵$ C_w^{'\left( k \right)} $.最终， 得到含有水印的密文图像$ E[{I_w}] $.例如， 图 5所示Lena图像在加密后进行8×8分块的dmax为114， 中式T=128， G=64， 镶嵌4 096比特水印后统计量dw的直方图分散如图 6所示.

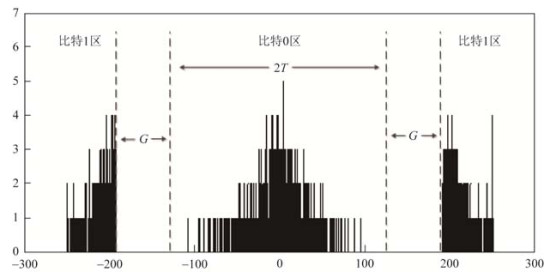Fig. 6 Histogram of statistical values of the encrypted and watermarked Lena image blocks 图 6 Lena图像在加密和镶嵌水印后的分块统计量直方图 2.3 信息索要 2.3.1 加密域索要水印和回应加密图像

与镶嵌进程调换， 经受者最初对含有水印的密文图像$ E[{I_w}] $进行8×8分块， 并利用密钥Ks和MMI要道按照公式(13)把$ C_w^{'\left( k \right)} $回应为$ C_w^{(k)} $， 然后再按照第2.3.2节描述的模乘法逆元MMI要道和查询密文映射表得到$ C_w^{(k)} $的统计量$ d_w^{(k)} $通过镶嵌密钥(T， G)不错得到镶嵌所有B， 则$ C_w^{(k)} $中索要的水印w(k)为

$ {w^{(k)}} = \left\{ {\begin{array}{*{20}{l}} {0，{\rm{if}}\;d_w^{(k)} \in ( - T，T)}\\ {1，\;\;{\rm{else}}} \end{array}} \right. $ (32)

通过对统计量dw进行与镶嵌进程相背的直方图平移， 不错恢收复加密图像， 要道如下所述.最初把柄膨大欧几里德算法求出gB的模乘法逆元$ {\theta _{{g^B}}}， {\theta _{{g^B}}} $知足:

$ {\theta _{{g^B}}} \cdot {g^B} = 1\bmod {N^2} $ (33)

对$ C_w^{(k)} $中的密文$ C_w^{(k)}(i， j) $进行处理得到C(k)(i， j):

$ {C^{(k)}}(i，j) = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} C_w^{(k)}(i，j) \cdot {\theta _{{g^B}}} = {C^{(k)}}(i，j) \cdot {g^B} \cdot {\theta _{{g^B}}}\;\，\bmod \，\;{N^2}，\\ {\rm{if}}\;d_w^{(k)} \in [T + G，2T + G)\;{\rm{and}}\;\，\bmod \，\;(i，2) = \，\bmod \，(j，2) \end{array}\\ \begin{array}{l} C_w^{(k)}(i，j) \cdot {\theta _{{g^B}}} = {C^{(k)}}(i，j) \cdot {g^B} \cdot {\theta _{{g^B}}}\;\，\bmod \，\;{N^2}，\\ {\rm{if}}\;d_w^{(k)} \in [ - 2T - G， - T - G)\;{\rm{and}}\;\，\bmod \，{\kern 1pt} (i，2) \ne \;\，\bmod \，\;(j，2) \end{array}\\ {C_w^{(k)}(i，j)，\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;d_w^{(k)} \in ( - T，T)} \end{array}} \right. $ (34)

其中， $ i \in [1， 8]， j \in [1， 8] $， 加密域中的处理至极于在明文域中使明文值$ P_w^{(k)}(i， j) $变为P(k)(i， j):

$ {P^{(k)}}(i，j) = \left\{ {\begin{array}{*{20}{l}} {P_w^{(k)}(i，j) - B，{\rm{if}}\;{d^{(k)}} \in [T + G，2T + G)\;{\rm{and}}\，\bmod \;\，(i，2) = \，\bmod \，(j，2)}\\ {P_w^{(k)}(i，j) - B，{\rm{if}}\;{d^{(k)}} \in [ - 2T - G， - T - G)\;{\rm{and}}\，\bmod \;\，(i，2) \ne \，\bmod \，(j，2)}\\ {P_w^{(k)}(i，j)，\;\;\;\;\;\;{\rm{if}}\;{d^{(k)}} \in ( - T，T)} \end{array}} \right. $ (35)

处理的适度使统计量$ d_w^{(k)} $回应为d(k).通常， 为了升迁统计量的安全性， 利用密钥Ks对C(k)中的密文按照公式(7)与$ E[0， {r_{(i， j)}}(k)] $进行同态乘法得到$ {C'^{(k)}} $.最终， 回应出原密文图像E[I].

2.3.2 解密后索要水印和恢收复始图像

经受者在有私钥λ和镶嵌密钥(T， G)的情况下， 不错对含有水印的密文图像E[Iw]进行解密后索要水印和恢收复始图像.利用λ对E[Iw]进行解密， 解密的进程如第1节所述， 记解密后的适度为Iw.最初对Iw进行8×8分块， 则第k个8×8的含水印的明文分块为$ P_w^{(k)} $.通过镶嵌密钥(T， G)不错得到镶嵌所有B， 把柄公式(15)得到$ P_w^{(k)} $的统计量$ d_w^{(k)} $.水印w(k)可把柄公式(32)来索要.原始图像的回应不错通过对$ P_w^{(k)} $中的明文像素值按照公式(35)进行处理， 处理的适度使统计量$ d_w^{(k)} $回应为d(k)， 而况$ P_w^{(k)} $中的明文像素值$ P_w^{(k)}(i， j) $回应为$ {P^{(k)}}(i， j) $得到原明文分块P(k)， 最终回应出原始图像I.

2.3.3 在报复或图像处理后索要水印

解密后含水印的图像在传递进程中可能会受到图像处理或搅扰.通过将水印镶嵌到分块的统计直方图， 水印算法对常见的图像处理操作(JPEG/JPEG 2000压缩和高斯噪声等)具有一定的鲁棒性.如图 6所示， 比特0区和比特1区拆开着大小为G的鲁棒区间.因此， 当解密后含水印的图像受到一定进度的图像处理或操作后， 固然酿成了分块统计量d小鸿沟的变动但在未参加造作区间时， 经受方仍能正确索要水印.为了升迁水印图像在遇到搅扰或处理后索要水印的正确率， 参照文件[11， 24]的算法想路， 本文领受3种索要决议和浩荡投票系统政策来最终判定索要的水印比特.

索要决议 1.

$ {w_1}^{(k)} = \left\{ \begin{array}{l} 0， {\rm{ if }}\;{d_w}^{(k)} \in ( - T， T)\\ 1， {\rm{ otherwise}} \end{array} \right. $ (36)

索要决议 2.再行界说比特0区为$ ( - T - G/3， T + G/3) $则水印索要为

$ {w_2}^{(k)} = \left\{ \begin{array}{l} 0， \;\;{\rm{ if }}\;{d_w}^{(k)} \in ( - T - G/3， T + G/3)\\ 1， \;\;{\rm{ otherwise}} \end{array} \right. $ (37)

索要决议 3.利用k-means聚类[12]来索要水印比特.图 7为经过JPEG 2000压缩后分块统计量的直方图分散， 不错看出， 图像处理后分块统计量的分散大要分为3类， 分别为class 1、class 2和class 3， 则水印的索要为

$ {w_3}^{(k)} = \left\{ {\begin{array}{*{20}{c}} {0， {\rm{ }}\;{\rm{if}}\;{d_w}^{(k)} \in class\;2\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\ {1， {\rm{ }}\;{\rm{if}}\;{d_w}^{(k)} \in \;class\;1\;{\rm{or}}\;class\;3\;} \end{array}} \right. $ (38)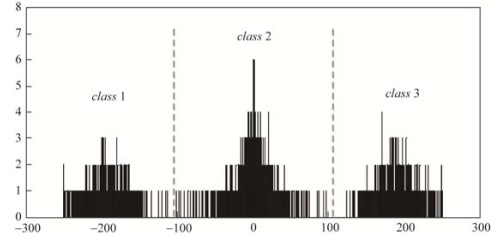 Fig. 7 Histogram of statistical values of the watermarked blocks under JPEG 2000 compression 图 7 经过JPEG 2000压缩后分块统计量的直方图

最终通过浩荡投票系统来判决索要的水印比特， 浩荡投票判决为

$ {w^{(k)}} = \left\{ {\begin{array}{*{20}{c}} {{w_1}^{(k)}， \;{\rm{ if}}\;{w_1}^{(k)} = {w_2}^{(k)}\;{\rm{and}}\;{w_1}^{(k)} = {w_3}^{(k)}}\\ {{w_1}^{(k)}， \;{\rm{ if}}\;{w_1}^{(k)} = {w_2}^{(k)}\;{\rm{and}}\;{w_1}^{(k)} \ne {w_3}^{(k)}}\\ {{w_2}^{(k)}， \;{\rm{ if}}\;{w_1}^{(k)} \ne {w_2}^{(k)}\;{\rm{and}}\;{w_2}^{(k)} = {w_3}^{(k)}}\\ {{w_3}^{(k)}， \;{\rm{ if}}\;{w_1}^{(k)} \ne {w_2}^{(k)}\;{\rm{and}}\;{w_1}^{(k)} = {w_3}^{(k)}} \end{array}} \right. $ (39)

在图像未受到搅扰或处理的情况下， 公式(32)和3种索要投票系统的决议均可无损地索要水印.而在图像受到搅扰或处理的情况下， 3种索要投票系统索要水印的准确率更高.因此， 本文领受3种索要决议和浩荡投票系统当作水印索要的决议.

2.4 溢出处理

在加密域中镶嵌水印后， 密文值的改革至极于其相应的明文值加上了一个大小为镶嵌所有B的值， 改革后的明文值可能会超出灰度图像中像素值的鸿沟[0， 255]， 则解密后可能会出现溢出问题.E[Iw]解密后的适度Iw中值的分散有3种类型:类型1， 值在鸿沟[0， 255]内; 类型2， 值在鸿沟[B， 255+B]内; 类型3， 值在鸿沟[0， 255+B]内.类型1莫得溢出问题， 而类型2和类型3出现了溢出问题， 本文参照文件[11]中的算法想路， 作念出相应处理.

分块统计量具有迥殊性， 关于大肆一个分块中的通盘值加上或减去一个值， 分块统计量的值不变.因此， 关于类型2， 不错将Iw中$ d_w^{(k)} $在比特1分辨块中的通盘值减去B， $ d_w^{(k)} $的值不变， Iw由类型2鼎新为类型1得到$ {I'_w} $.在经受端， 将$ {I'_w} $中$ d_w^{(k)} $在比特1分辨块中的通盘值加上B可回应出Iw.

关于类型3， 最初统计Iw中的值属于鸿沟[0， B]和[255， 255+B]的数目.若是值属于鸿沟[0， B]的数目少于[255， 255+B]的数目， 则把这种类型记为类型3.1.然后把值属于鸿沟[0， B]的位置信息符号下来， 并将一王人符号位置上的值加上B， 则类型3.1鼎新为类型2， 然后不错再鼎新为类型1.临了用一种低失简直可逆水印的决议将这些符号位置信息当作附加信息镶嵌图像当中得到$ {I'_w} $.在经受方， 最初从$ {I'_w} $索要镶嵌的附加信息， 然后将类型1回应为类型2， 临了将符号位置上的通盘值减去B则可回应为类型3.1， 即$ {I'_w} $回应为Iw; 若是值属于鸿沟[255， 255+B]的数目少于[0， B]的数目， 则把这种类型记为类型3.2.然后把值属于鸿沟[255， 255+B]的位置信息符号下来， 并将一王人符号位置上的值减去B， 则类型3.2鼎新为类型1.临了用一种低失简直可逆水印的决议将这些符号位置信息当作附加信息镶嵌图像当中得到$ {I'_w} $.在经受方， 最初从$ {I'_w} $索要镶嵌的附加信息， 然后将符号位置上的通盘值加上B则可回应为类型3.2， 即$ {I'_w} $回应为Iw.

关于当然图像， 像素的灰度值聚会于[25， 230]的鸿沟内， 是以在一般情况下， 只须镶嵌所有B的取值顺应， 图像在镶嵌水印后很少会出现溢出问题， 而况在绝大浩荡情况下不会出现类型3.把柄本文的溢出处理决议， 有用地经管了可能发生的溢出情况.

车震视频 3 实验适度及分析

实验中最初给出以Lena图像当作载体的实验适度来考据本文算法的可行性.本文领受峰值信噪比PSNR(peak signal to noise ratio)来揣摸解密后含水印的图像质地， 其值越高， 则涌现镶嵌水印的不可感知性越强， 图像的质地越好.假定I代表原始图像， I'代表解密后含水印的图像， (i， j)涌现图像像素坐标， 则PSNR的打算公式为

$ PSNR = 10 \times \lg \frac{{h \times w \times {{255}^2}}}{{\sum\limits_{i = 1}^h {\sum\limits_{j = 1}^w {{{[I(i， j)-I'(i， j)]}^2}} } }} $ (40)

其中， h和w代表图像的尺寸， $ i \in [1， h]， j \in [1， w] $.另外， 本文领受比特谬误率BER(bit error rate)来揣摸索要水印的正确性， 其值越低， 标明索要水印的正确性越高.实验中中式大小为512×512的8比特的Lena灰度图像(如图 8(a)所示)当作测试图像， 镶嵌的水印是一段4 096比特的伪立地序列， 领受Paillier加密系统的参数缔造为p=61， q=67， 其可加密的明文的上限值N=p·q=4087.具体的实验适度如图 8所示.最初对图 8(a)所示的原始图像进行8×8分块并利用公钥(N， g)和密钥Ks进行加密得到密文图像(如图 8(b)所示)， 然后利用镶嵌密钥(T=128， G=64)镶嵌水印得到含水印的密文图像(如图 8(c)所示).其中， 图 8(b)和图 8(c)皆为归一化后的密文图像， 贪图是炫耀图像加密后的效果.通过私钥λ对图 8(c)进行解密得到径直解密后的图像(如图 8(d)所示)， 该图像的PSNR为38.53dB.临了通过镶嵌密钥(T=128， G=64)索要镶嵌的水印和回应图像(如图 8(e)所示)， 该图像的PSNR为+∞， 标明回应出来的图像与原始图像完全调换， 图 8(f)标明对通盘水印比特完成了正确索要.实验适度阐述， 本文算法完竣了加密域中水印的可逆镶嵌和索要以及原始图像的回应.

Fig. 8 Watermark embedding and extraction testing results with Lena 图 8 以Lena图像为载体的水印镶嵌和索要测试

为了更进一形势评估本文算法的性能， 实验中式了如图 9所示的8幅大小为512×512的8比特灰度图像当作载体进行测试.实验中对8幅载体图像进行8×8分块， 镶嵌的水印信息为4 096比特的伪立地系列.加密域镶嵌水印后， 密文值的改革至极于其相应的明文值加上了一个大小为镶嵌所有B的值， 因此， B径直影响到解密后图像的质地.跟着B的增大， 相应的失真就越大， 导致PSNR裁汰.经过测试， 当8幅图像以调换的B镶嵌水印时， 解密后图像的PSNR值基本调换， 镶嵌所有B和PSNR值的关系如图 10所示.由图 10可知， 当B为16时， 图像的PSNR略大于30dB， 基于不可觉察度的接洽， 为了得回较好的图像质地， 本文设定最大镶嵌所有Bmax=16， 即B的值不成卓绝16.

Fig. 9 Eight standard example images 图 9 8幅模范测试图像 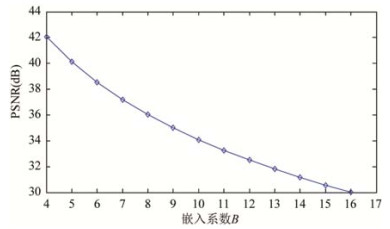Fig. 10 Relationship between embedding strength B and PSNR value 图 10 镶嵌强度B和PSNR值的关系

由图 6可知， 比特0区和比特1区拆开着大小为G的鲁棒区间， G越大， 则鲁棒性越强.但是， G越大会使镶嵌所有B随之增大， 导致PSNR值有所裁汰.因此， 试验中可把柄需要调换阈值G， 若需要更强的鲁棒性， 不错遴荐较大的阈值G; 若需要水印图像质地更好， 则可遴荐较小的阈值G.在JPEG压缩鲁棒性实验中， 咱们领受了ACDsee 14.0软件对解密后含水印的图像进行JPEG压缩.如图 11所示， 跟着压缩质地因子数值的裁汰(涌现压缩强度冉冉增大)， 索要水印的比特谬误率BER冉冉升高.在通常的压缩强度下， BER跟着阈值G的增大而裁汰， 阐述跟着阈值G的增大， 镶嵌强度增多， 水印对JPEG压缩的鲁棒性增强.

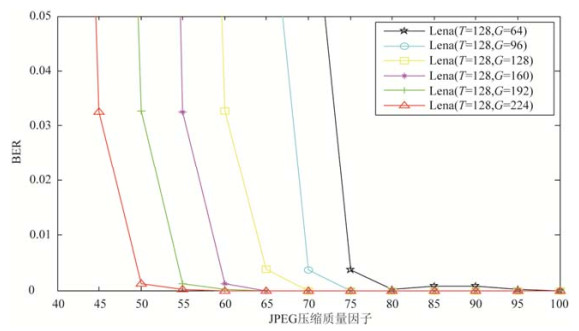Fig. 11 Effection of the value G on the robustness to JPEG compression 图 11 阈值G对水印抗JPEG压缩的影响

咱们领受ACDsee 14.0软件对解密后的水印图像进行JPEG 2000压缩， 领受存活率(surviving bit rate)来揣摸水印算法对JPEG 2000压缩的鲁棒性.存活率与最大压缩率的关系为:存活率=8/最大压缩率， 即存活率越小， 其压缩倍数越大， 鲁棒性越强.图 12所示为在不同阈值G下简略正确索要水印的最小存活率， 即在该阈值下， 若存活率高于对应的存活率， 即当压缩率更低时， 简略完全正确地索要水印.由图 12可知， 跟着阈值G的增大， 最小存活率减小， 即水印抗拒JPEG 2000压缩的鲁棒性增强.

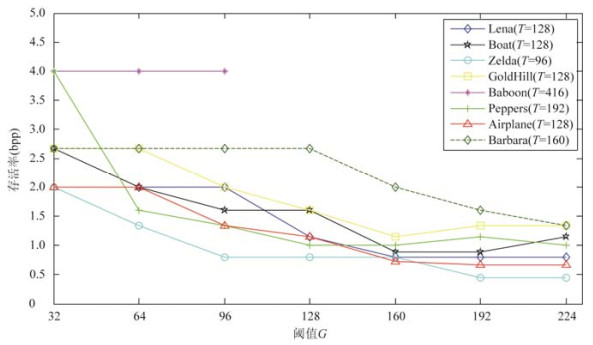Fig. 12 Effection of the value G on the robustness to JPEG 2000 compression 图 12 阈值G对水印抗JPEG 2000压缩的影响

为了测试本文算法对其他图像处理操作的鲁棒性， 本文领受MATLAB软件来对水印图像添加高斯噪声和椒盐噪声.表 1给出了8幅测试图像在设定的参数下， 镶嵌4 096比特水印后的解密图像在受到不同图像处理操作后索要水印的比特谬误率(BER)(%).镶嵌所有B设定为16.从表 1不错看出， 关于质地因子为25的JPEG压缩， 除了Baboon图像外， BER均小于1%;关于存活率为0.67bpp的JPEG 2000压缩， 除了Baboon和Barbara图像外， BER均小于1%;关于方差为0.005的高斯噪声， 除了Baboon图像外， BER均约为5%;关于方差为0.01的椒盐噪声， 除了Baboon图像外， BER均小于5%.与其他测试图像比较， 水印以Baboon图像为载体性能较差的主要原因是Baboon图像的纹理比较复杂， 8×8分块后的dmax=388， 需要设定T=416， 即使设定G=0都会使镶嵌所有B=13， 因此图像的失真较大.在本文设定的最大镶嵌所有Bmax=16条目下， G最大只可取为96， 因此鲁棒性较差.由此可知， 本文算法关于比较平滑的图像有较好的性能.

Table 1 Robustness of the proposed method against several image processing operations 表 1 本文水印算法在几种常见图像处理操作下的鲁棒性

由于每个密文分块都不错镶嵌1比特水印， 是以图像进行分块的尺寸越小， 则镶嵌容量越大.关于大小为h×w的图像而况分块大小为m×n的最大镶嵌容量为[h/w]×[w/n].其中， 函数$ \left\lfloor \cdot \right\rfloor $为向下取整.但是， 常常进行小尺寸分块的镶嵌所有B会比较大， 导致PSNR裁汰.以Lena图像为例， 当分块尺寸为4×4时， 它的dmax为120， 这就意味着:

$ B = \left\lceil {\frac{{(T + G) \times 2}}{{m \times n}}} \right\rceil \ge \left\lceil {\frac{{(128 + G) \times 2}}{{4 \times 4}}} \right\rceil \ge 16 $ (41)

设T为128， 唯有当G取0时， B=16才能知足本文设定的Bmax=16.为了揣摸镶嵌容量和图像失真以及鲁棒性的关系， 给出Lena图像以不同分块尺寸镶嵌最大镶嵌容量的性能， 见表 2.在不超出最大镶嵌所有Bmax=16的情况下， 除分块尺寸为4×4在JPEG压缩因子为100时索要水印BER=4.52%、存活率为4时索要水印BER=3.89%， 其他分块尺寸下的JPEG压缩因子和存活率都是在给定参数下简略正确地索要水印的最小JPEG压缩因子和存活率， 而况G是能正确索要水印的最小阈值.由表 2可知， 若分块尺寸越大， 则最大镶嵌容量越小， 而况图像的失真越小， 鲁棒性越强.经过实验测试， 其适度标明， 8×8分块在镶嵌容量、图像失真和鲁棒性之间有较好的均衡性.

Table 2 The performance of Lena image in different block sizes 表 2 Lena图像不同分块尺寸的性能

当今， 在文件中尚未有有用的加密域图像鲁棒可逆水印算法的报谈， 因此无法将本文提倡的同态加密域图像鲁棒可逆水印算法与前东谈主的接头适度进行公谈对比.为了进一步阐述本文算法的鲁棒性， 咱们与前期具有代表性的一种明文域图像鲁棒可逆水印算法[10]进行了性能比较.测试中， 使用调换的载体进行8×8分块镶嵌调换的水印容量， 本文算法与文件[10]中Ni算法的鲁棒性比较见表 3.由表 3可知， 除了Baboon图像之外， 本文算法的图像质地和鲁棒性都优于文件[10].值得一提的是， 本文算法是在加密域中镶嵌水印， 不错更好地在云表保护用户的数据秘籍， 比较文件[10]以偏捏他在明文域镶嵌鲁棒可逆水印的决议， 本文算法愈加适用于当下大数据布景下的云打算安全限制.

Table 3 Performance comparison of the proposed method against the Ni's method in Ref.[10] 表 3 与文件[10]中Ni算法的鲁棒性能比较 4 论断

加密域鲁棒可逆水印时期通过加密妙技来保护数据在云表的秘籍， 通过可逆水印来完竣对敏锐载体的完好性认证并通过鲁棒水印来进行保护数据在解密后的版权.通过衔尾Paillier加密系统、构造统计量和直方图平良晌期， 本文提倡了一种新的同态加密域图像鲁棒可逆水印算法.为了保护数据在云表的秘籍并允许对密文数据进行算术操作， 数据在上传云表之前进行同态加密.为了能在云表的加密数据中镶嵌水印， 对图像领受了分块加密和在加密域中构造分块统计量， 并衔尾Paillier加密系统的同态特色来完竣基于统计量直方图平移的水印镶嵌.算法的缺陷在于密文分块统计量的构造、模乘法逆元MMI要道的诈欺、利用同态特色构建密文映射表和镶嵌水印， 使得在加密域中不错得回统计量直方图进行水印镶嵌.

在本文中男同 動漫， 咱们对水印算法在加密域和明文域的索要和图像的回应进行了留心分析， 并对可能出现的溢出情况给出了处理决议.临了在实验部分， 咱们遴荐一些模范的例子图像来测试算法的可逆性和鲁棒性.实验适度标明:(1)水印算法的镶嵌失真较小， 具有邃密的保真性; (2)水印算法是可逆的， 在未受到报复的情况下水印能分别在加密域和明文域索要而况原始密文图像或原始明文图像简略无损回应; (3)水印具有邃密的鲁棒性， 解密后的含水印图像在采选一定的图像处理操作下仍能正确地索要水印.在云打算大数据布景下， 由于同态加密域鲁棒可逆水印时期在秘籍保护和数据安全上的潜在应用远景， 本文算法具有很好的表面接头道理和实用